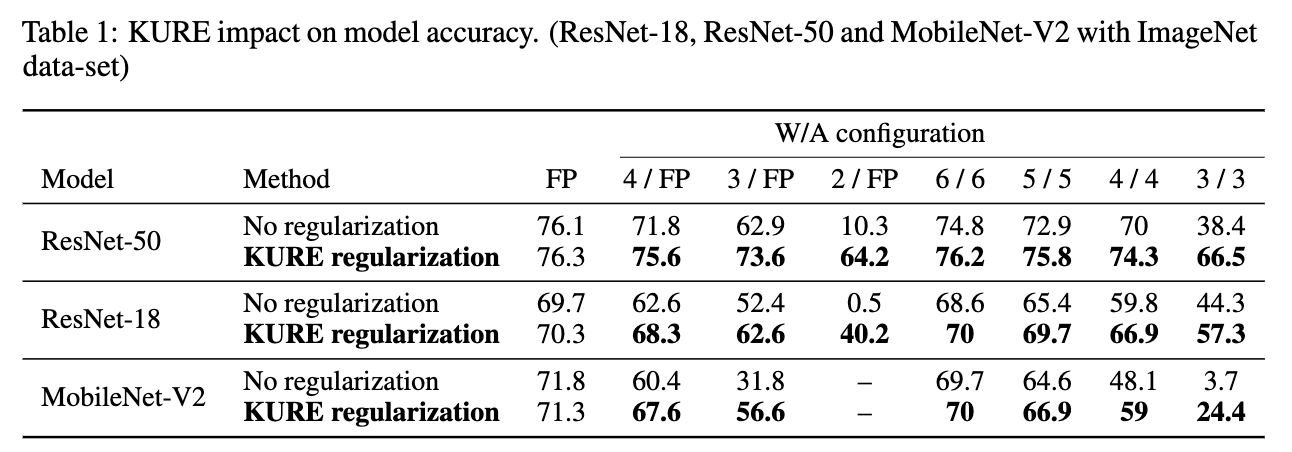
Robust Quantization: One Model to Rule Them All

2024-01-15

Keywords: #Quantization

---

0. Abstract

• Issue: Quantization process is not static and can vary to meet different circumstances and implementations.
• Proposal: A single generic model capable of operating a various bit-widths and quantization policies.

1. Introduction

• QAT: Simulate quantization arithmetic on the fly
• PTQ: Quantize the model after the training while minimizing quantization noise.
• Quantizer Implementations: 1) Rounding Policy, 2) Truncation Policy, 3) The quantization step size adjusted to accommodate the tensor range
• Proposal: A generic method to produce robust quantization models. KURE- A KUrtosis REgularization term, added to the model loss function.
• Contribution
  1. Prove that uniformly distributed weight tensors have improved tolerance to quantization with higher SNR, and lower sensitivity to specific quantizer implementation.
  2. KURE- a method to uniformize the distribution of weights
  3. Apply KURE to ImageNet models and demonstrate that generated models can be quantized robustly in both PTQ and QAT regimes.

2. Related Work

• Robust Quantization
  • (Alizadeh et al., 2020) Penalizing the L1 (norm of gradients), which requires running the backprop twice.
  • Our work promotes robustness by penalizing fourth central moment (Kurtosis), which is differentiable/trainable.
  • We demonstrate robustness to a broader range of conditions e.g. change in quantization parameters as opposed to only changes to different bit-widths.
  • Our method applies to both PTQ and QAT while (Alizadeh et al., 2020) focuses on PTQ.
• Quantization methods
  • As a rule, these works can be classified into two types:
    1. post-training acceleration
    2. training acceleration
  • Both suffer from one fundamental drawback- they are not robust to variations in quantization process or bit-widths other than the one they were trained for.

3. Model and Problem Formulation

• MSE is the local distortion measure we would like to minimize
• With respect to small changes in the optimal quantization step size, we measure the difference (sensitivity).
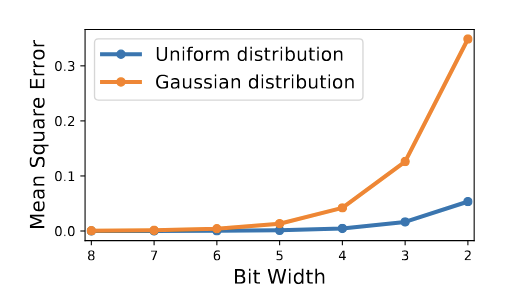
• We use Lemma 1 to compare the quantization sensitivity of the Normal dist. with Uniform dist.

3.1 Robustness to varying quantization step size (?)

• We show that for a tensor $X$ with a uniform distribution $Q(X)$ the variations in the region around $Q(X)$ are smaller compared with other typical distributions of weights. → Ambiguous- uniform $X$, or uniform $Q(X)$?

• Normally distributed: Sensitivity zeros only asymptotically when ∆ (and MSE) tends to infinity. This means that optimal quanti-zation is highly sensitive to changes in the quantizationprocess.
• Uniformly distributed: The optimum ˜∆ is attainedat a region where quantization sensitivity Γ(X_U , ε) tends to zero. This means that optimal quantization is tolerant and can bear changes in the quantization process without significantly increasing the MSE.

3.2 Robustness to varying bit-width sizes

• MSE distortions for different bit-width whwen normal and uniform distributions are optimally quantized.

3.3 When robustness and optimality meet

• For the unifom case, the optimal quantization step size in terms of $MSE(X, \tilde{\delta})$ is generally the one that optimizes the sensitivity.
• The second order derivative w.r.t $\delta$ for sensitivity zeroes at approximately the same location as the optimal quantization step size for MSE.

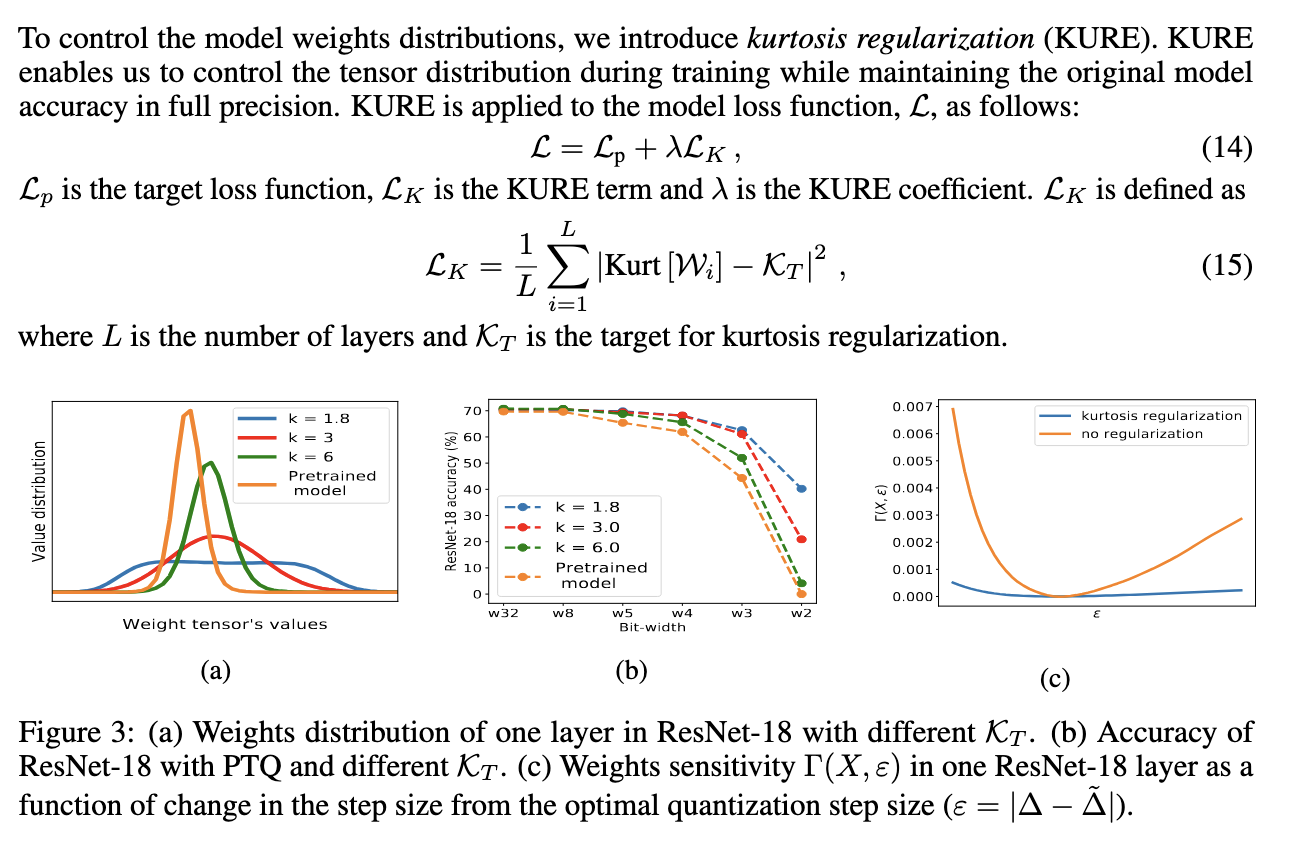
4. Kurtosis regularization (KURE)

• We use kurtosis- the fourth standardized moment- as a proxy to the probability distribution

4.1 Kurtosis- The fourth standardized moment

• Kurtosis of a random variable $\mathcal{X}$

• If $\mathcal{X}$ is uniformly distributed, its kurtosis value will be 1.8, whereas if $\mathcal{X}$ is normally of Laplace distributed, its kurtosis values will be 3 and 6, respectively.
• We define “kurtosis target” $\mathcal{X}_T$, as the kurtosis value we want the tensor to adopt.
• In this case, the kurtosis target is 1.8 (uniform distribution)

4.2 Kurtosis Loss

• Kurtosis Loss

• Everything below is important

5. Experiments

---