SmoothQuant: Accurate and EfficientPost-Training Quantization for Large Language Models

2024-01-20

Keywords: #Quantization

---

0. Abstract

• SmoothQuant: A training-free, accuracy-preserving, and general purpose PTQ solution to enable 8-bit weight, 8-bit activation (W8A8)
• General Idea: Weights are easy to quantize while activations are not. SmoothQuant smooths the activation outilers by offline migrating the quantization difficulty from activations to weights with a mathematically equivalent transformation.

1. Introduction

• Problem: Activations of LLMs are difficult to quantize because of systematic outliers with large magnitude. → A training-free quantization scheme for LLMs that would use INT8 for all the compute-intensive operations remain an open challenge.
• Key Observation: Even if activations are much harder to quantize than weights due to outliers, different tokens exhibit similar variations across their channels. → SmoothQuant offline migrates the quantization difficulty from activations to weights
• Contribution
  1. Proposes a mathematically equivalent per-channel scaling transformation that significantly smooths the magnitudes across channels (?)
  2. Compatible with various quantization schemes
  3. Hardware-efficient
  4. Easy to implement

2. Preliminaries

Quantization: Integer uniform quantization, assume input tensor is symmetric at 0 for simplicity.

• Quantizers uses maximum absolute value to calculate $\Delta$, so that it preserves outliers in activation.
  • Static quantization: Calculate $\Delta$ offline with the activations of some calibration samples.
  • Dynamic quantization: Use runtime statistics of activations to get $\Delta$. $\Delta$ is learned on the fly.
• Quantization Granularity
  • per-tensor: Uses a single step size for the entire matrix
  • per-token (per-channel): Uses different step sizes for activations associated with each token (each channel)
  • group-wise quantization: A coarse-grained version of per-channel quantization, uses different quantization steps for different channel groups
• Why does W8A8 need to be achieved?
  • Storage is reduced by half when quantizing FP16 to INT8.
  • To speed up inference, we need to utilize the integer kernels (e.g., INT8 GEMM) supported by a wide range of hardware → we need to quantize both weights and activations into INT8 (W8A8)

3. Review of Quantization Difficulty

We first review the difficulties of activation quantization and look for a pattern amongst outliers.

1. Activations are harder to quantize than weights. The weight distribution is quite uniform and flat.
2. Outliers make activation quantization difficult. Large outliers dominate the maximum magnitude measurement, leading to low effective quantization bits/levels for non-outlier channels.
3. Outliers persist in fixed channels
   • Outlier appear in a small fraction of the channels → Variance amongst the channels for a given token is large
   • If one channel has an outlier, it persistenly appears in all tokens → Variance between the magnitudes of a give channel across tokens is small (Figure, red)
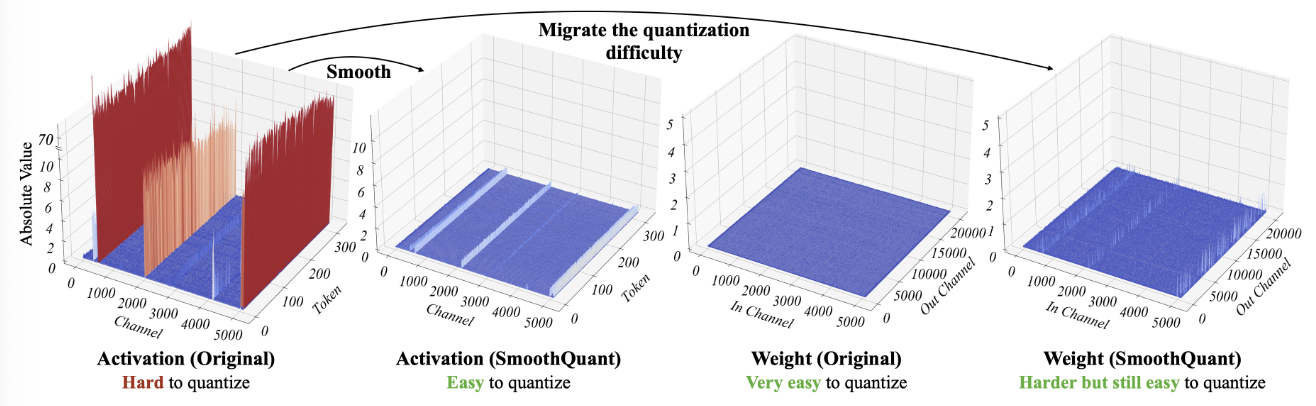
   • per-channel quantization would be preferred over per-token quantization
   • However, per-channel activation quantization does not map well to hardware-accelerated GEMM kernels, because scaling can only be performed along the outer dimensions of the MM.
   • This is why previous works all use per-token activation quantization, even though it cannot address the difficulty of activation quantization and shows only slightly better performance than per-tensor.

4. SmoothQuant

Per-channel activation quantization is infeasible. We propose to “smooth” the input activation by dividing it by a per-channel smoothing factor. Input is usually produced from previous linear operation, we can easily fuse the smoothing factor into previous layers’ parameters offline.

Migrate the quantization difficulty from activations to weights.

• We aim to choose a per-channel smoothing factor $s$ such that $\hat{X}=X\text{diag}(s)^{-1}$
• To reduce quantization error → increase the effective quantization bits for all channels.
• The total effective quantization bits would be largest when all channels have the same maximum magnitude.
• Straight-forward choice is $s_j=\max{(|X_j|)}$ in $j$-th input channel.

• On the other hand, push all the quantization difficulty from weights to activations by choosing $s_j=1/\max{(|X_j|)}$

• Problem: This formula pushes all the quantization difficulties to the weights.
• Therefore, we split the quantization difficulty between weights and activations so they are both easy to quantize. → hyper-parameter “migration strength $\alpha$” to control how much difficulty we want to migrate from activation to weights using the following equation.

• The formula ensures that weights and activations at the corresponding channel share a similar maximum value, thus sharing the same quantization difficulty.

5. Experiments

5.1 Setups

Baselines.

---