Skip to main content Link Menu Expand (external link) Document Search Copy Copied

Any-Precision LLM: Low-Cost Deployment of Multiple, Different-Sized LLMs

2024-05-23


Keywords: #Flexiblebitprecision #CUDA

0. Abstract

  • We propose any-precision quantization of LLMs, leveraging a PTQ framework
  • We develop a specialized software engine for its efficient serving. ➡ Our solution significantly reduces the high costs of deploying multiple, different-sized LLMs, by overlaying LLMs quantized to varying bit-widths into a single $n$-bit LLM.

1. Introduction

  • Main problem: Limited discussion on mitigating the costs associated with deploying multiple LLMs of varying sizes.
    1. It exacerbates the already high memory costs of LLM deployment
    2. It necessitates training of multiple model versions when models of desired sizes are not readily available as open-source.
  • Any-precision LLM: Utilization of multiple LLMs with varying sizes by storing only a single large LLM ($n$-bit model) in memory, while avoiding the additional overhead of training multiple LLMs.
    • Any-precision DNN: $n$-bit quantized model capable of generating lower bit quantized models simply by taking its MSBs.
  • Two challenges of Any-precision LLM
    1. A practical for any-precision quantization of LLM is needed.
    2. A new GPU kernel for quantized matrix-vector multiplication is required, which will translate the use of reduced bit-widths in any-precision LLMs into shorter inference times. ← With existing kernels, opting for a model with a lower bit-width does not reduce memory bandwidth usage.
  • Contributions
    1. Packs LLMs quantized to varying bit-widths, such as 3, 4, .. up to $n$ bits, into a memory footprint comparable to a single $n$-bit LLM.
    2. Despite having to adopt a bit-interleaved (bitplane) memory layout for the support of any-precision, showcases high inference throughput.

2. Background

2.1. GPU Basics

  • GPU: Comprises a large number of processing elements called SMs.
  • GPUs include multi-level on-chip SRAM caches. Part of the L1 cache can be configured as shared memory, a memory space that can be directly controlled by programmers.
  • GPUs use a large number of threads to execute kernels.
  • Threads are structured into thread blocks, while these are further organized into a set of warps, with each warp consisting of 32 consecutive threads.
  • All threads within a thread block share the same shared memory space.
  • All threads within a warp execute the same instruction at the same time.

2.2. LLM Quantization

  • Weight-only PTQ: The dominant bottleneck in inference throughput is the memory constraint imposed by the size of weight parameters, rather than computational requirements. QAT is impractical since it has high training expense.
  • GPTQ: A pioneering work on weight-only PTQ for LLM
  • SqueezeLLM proposes a clustering-based LLM quantization that considers the sensitivity of each weight. (non-uniform quantization)

3. Motivation

3.1. Need for deploying multiple, different-sized LLMs

  • Enhance user experience by effectively handling queries with varying latency requirements.
  • Speculative decoding: Necessitates multiple LLMs of varying sizes

3.2. Challenges of deploying multiple, different-sized LLMs

  1. Memory Overhead: As LLMs are typically substantial in size, maintaining even a few additional smaller models incurs significant costs
  2. Training Costs
    • Most open-source LLMs offer only one to three variants of parameter counts.
    • Training an LLM is very costly due to its high computational needs and large corpus requirement.
    • corpus: A collection of written or spoken material is used to train the language model

3.3. Our Solution: Any-Precision LLM

  • Concept
    • Any-precision: Highly memory-efficient as it allows the utilization of varying bit-width models by only storing in memory 1) the quantized weights of the parent model, and 2) a set of quantizataion parameters (centroid values)
    • Separate deployment: Models of different bit-widths requiring the deployment of separate models, each taking up its own memory space.
  • Challenges of Any-Precision LLM
    1. QAT scheme requires models to be trained from scratch: For LLMs, training is not affordable to most users
    2. Any-Precision has no regard for memory bandwidth savings: The entire $n$-bit parameters of the parent model are loaded into memory, only then being further quantized into lower bit-width weights by bit-shifting as needed.
      • Any-Precision strategy makes sense for CNN models, because they are compute-bound. ↔ LLM inference is highly memory-bound due to its low arithmetic intensity, and the Any-Precision does not offer any benefits in terms of memory bandwidth.
      • Memory load of weight parameters is the single primar performance bottleneck. → We incorporate both a low-cost any-precision quantizationi mehthod and a specialized software engine wherein reduced precision inference directly translates to actual speed-ups.

4. Any-Precision Quantization for LLM

4.1. Incremental Upscaling

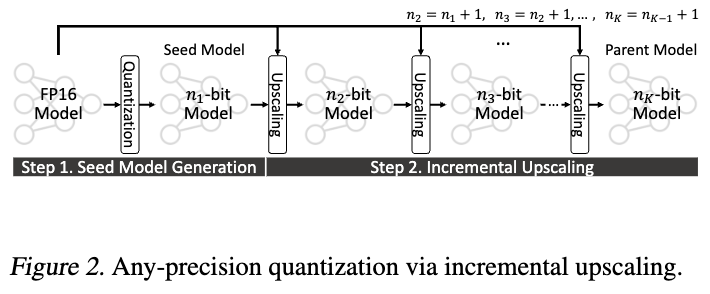
  1. Quantizes the model to the minimum supported bit-width ($n_1$) = seed model
  2. Incrementally upscale one bit at a time, until we obtain the final $n_K$-bit parent model.
    • For every incremental upscale from $n_i$-bit model to an $n_{i+1}$-bit model; all params of the $n_i$ bit model are inherited to the $n_{i+1}$-bit model, and a single additional bit is appended to end of each param.

4.2. Non-uniform Quantization-based Incremental Upscaling

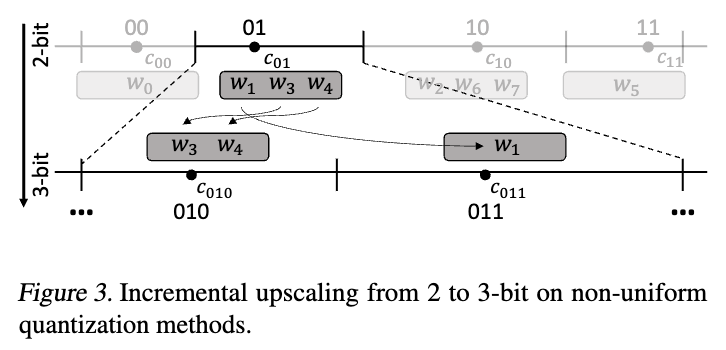
5. Specialized Software Engine

5.1. Need for New Software Engine

  • Existing GPU kernels:
    • GDDR (Graphics Double Data Rate, [S]DRAM, synchronous dynamic ram, different from static ram SRAM) ↔️ L1 cache in each SM: 64B (1.0~1.3, 64bx8burst=64B cache line), 32B (2.0~)
    • L1 cache ↔️ SP cache line: 128B
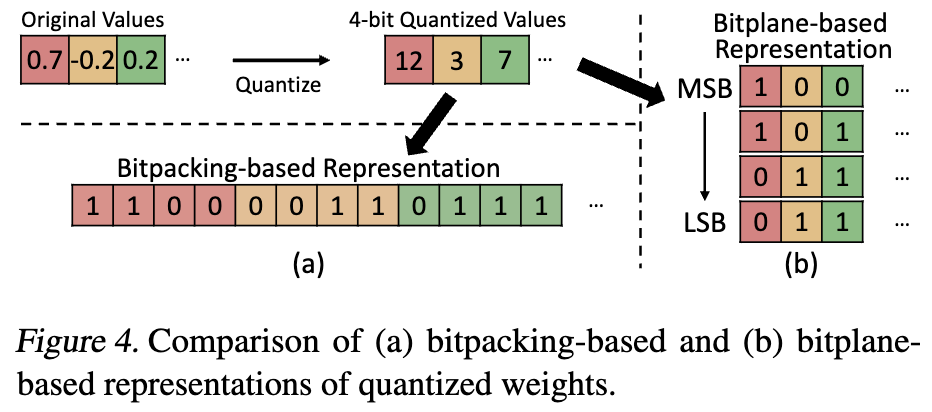
  • Bitpacking: Store quantized weights sequentially in a 1-D array. With this representation, the entire weight array has to be loaded even when running a model in a reduced bit-width.
    • For example in Figure 4-(a), even when executing a 2-bit or 3-bit model, the full 4-bit values have to be read from memory.
    • This is because of the coarse-grained memory access granularity of GPUs, typically 128B.
  • Bitplane: Decomposes quantized weights into $n$ bit-vectors, where $n$ is the bit-width. Each bit-vector is formed by taking each bit position of the quantized values. (2-D array, cut off the LSBs -> return 1-D array)
    • Any runtime request of reduced bit-width directly translates into proportional speedup, as we can simply load the specified amount of bits.
  • Bitplane-based representation is relatively common in CPU GEMM, but not in GPUs.
  • Why we can’t use LUT-GEMM
    • Lacks support for any-precision as it necessitates of distinct weight layouts to accommodate different bit-widths.
    • LUT-GEMM strictly requires weights to adhere to BCQ (binary-coding quantization)- BCQ can’t support the codebook-based non-uniform quantization method

5.2. System Overview

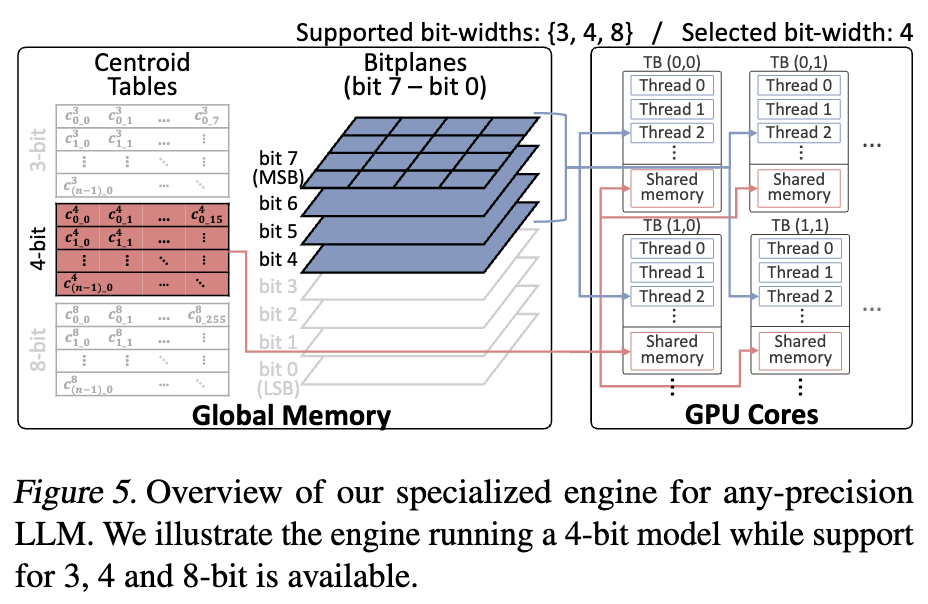
  • Centroid tables and bitplanes are stored in global memory.
  • Centroid tables have rows equal to the number of output channels, with each row containing $2^k$ values (representing each value $k$ bits can represent), where $k$ refers to the bit-width.
  • The rows of the centroid table are scattered across the shared memory

  • The threads load non-overlapping regions of the weight bitplanes

  • Thread-Level Operations
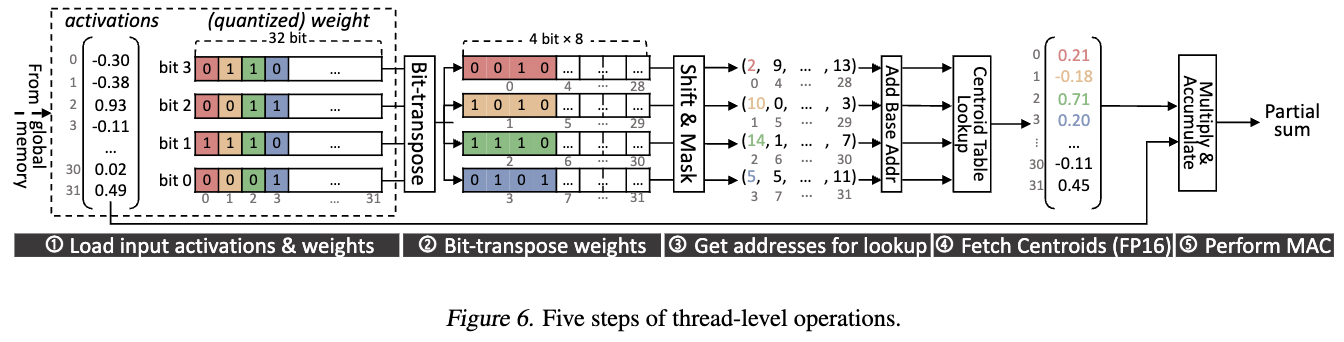    (Assuming bit-width of 4)
    1. Each thread warp thread loads 32 input activations with their corresponding weights (four 32bit bit-vectors)
    2. Bit-vectors are rearranged so that the bits of each weight align contiguously. = Bit-transpose of eight 4-by-4 bit matrices
    3. Bit-transposed bit-vectors are shifted & masked to obtain the indices for centroid lookup.
    4. Dequantization: Fetching centroids from the table in the shared memory
    5. MAC

5.3. GPU Kernel Optimization

  • GPU kernel optimization techniques aimed at addressing inefficiencies stemming from the characteristics of bitplane-based quantized GEMM

❥ Weight Bitplane Layout Optimization

  • It is preferable for all threads in a warp to access consecution memory locations- for coalescing
  • Problem: CUDA limits per-thread max load size = 16B (where granularity for all 32 threads = 128B)
    • Weight: 1b; as they are in bitplane
    • Activation: 16b; as they are FP16
    • Because of this size difference, and per-thread max load size restriction → coalescing can’t be done for activation
  • Optimization: Permuting bytes in the weight bitplanes to ensure that threads access activations in a coalesced manner.
    • The indices of weights accessed by each thread are no longer sequential → doesn’t matter because it is still coalesced access
  • Question: Global access for weights increase 4 times than before optimization
    • It’s okay, since it already reuires four memory accesses to load the activations
    • No, it’s not because weights take 4 times for every bitplane

❥ Efficient Bit-Transpose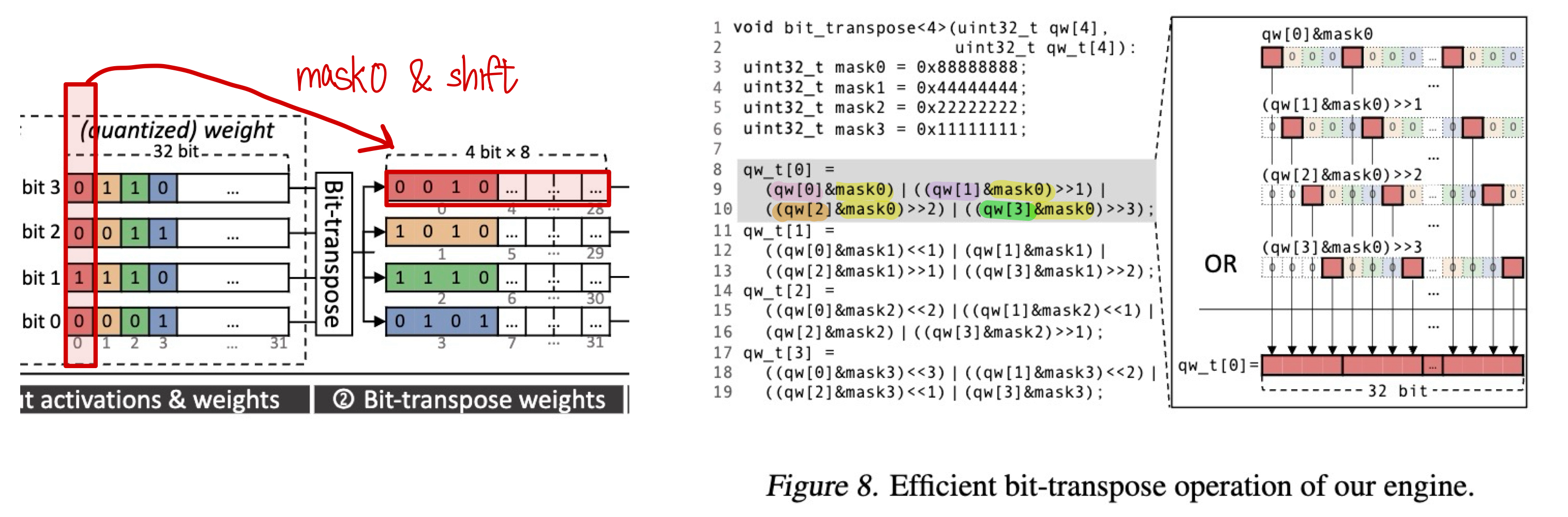

  • Problem: The bit-transpose step is the main overhead amongst the large number of bitwise operations.
    • Most widely used bit-transpose algorithm requires 38 bitwise ops. for 8x8 bit matrix
  • Optimization: Treat 32b bit-vector = 8 x 4b sub-bit-vectors
    • 40 bitwise ops. = (6shifts + 4 ands) * 4b positions < 76 ops for 8x8 bit matrix twice
    • For non-power-of-2 bit-widths: Use the next larger bit-width that is a power of 2 (with padding, perhaps) → Shouldn’t matter, memory storage is in the format of bitplane, it only requires more space after memory access

❥ Merging Table Lookups

  • Problem: Bitwise operations for the centroid table index calculation (Step 3 in Figure 6) can also become a bottleneck, particularly at small bit-widths.

6. Evaluation

  1. Quantized models generated from incremental upscaling + non-uniform quantization match SOTA at their respective bit-widths
  2. Our specialized engine matches/outperforms existing engines while providing memory-efficient any-precision support.

6.1. Any-Precision Quantization Results

  • Methodology: We evaluate 4 to 8-bit models obtained through incremental upscaling, using a 3-bit SqueezeLLM model as the seed model
    • Compete with 4 to 8-bit SqueezeLLM
    • Benchmark:
    • Evaluation metrics: Perplexity, zero-shot accuracies
  • Results: With just single $n$-bit parent model generated through the incremental upscaling process, we can utilize the full range of 3 to $n$-bit models.