NoisyQuant: Noisy Bias-Enhanced Post-Training Activation Quantization for Vision Transformers
2024-07-02
Keywords: #PTQ #noise #activationdistribution
0. Abstract
- Heavy tailed distribution of ViT activations is the problem!!
- Proposal: For a given quantizer, adding a fixed Uniform noisy bias to the values being quantized can significantly reduce the quantization error under provable conditions.
1. Introduction
- ViT compression and acceleration methods: Pruning, quantization, NAS, etc.
- QAT vs PTQ
- QAT: Finetunes the quantized model → High training cost, complicated computation graph of ViT
- PTQ: No need for re-training or finetuning the quantized model, instead only adjusts the design of the quantizer based on the full-precision pretrained model & a small set of sampled calibration data.
- Activation Quantization for ViT
- Outputs of the GELU function are asymmetrically distributed, with spikes in the histogram at some values and a long tail in a large range. (top-left of Fig. 1)
- No linear uniform PTQ method achieves good performance on vision transformer models
- A new perspective
- Instead of adding more tricks in the quantizer design to fit the activation distribution, let’s alter the distribution being quantized, making it more friendly to a given quantizer! → In other words, let’s not make the quantizer do all the work; Offload some of the work by making the dist. friendlier for the quantizer
- How? For any quantizer, the quantization error can be significantly reduced by adding a fixed noisy bias sampled from a Uniform distribution to the activation before quantization.
- Steps to NoisyQuant
- Sample Noisy Bias based on the input activation dist. following our theoretical analysis.
- Compute the corresponding denoising bias to retain correct output of the layer.
- At inference time, Noisy Bias is added to the input activation before quantization.
- Denoising bias is removed from the layer output.
- Proposal
- Theoretically shows the possibility and proves feasible conditions for reducing the quantization error of heavy-tailed distributions with a fixed additive noisy bias
- Proposes NoisyQuant, a quantizer-agnostic enhancement for PTQ performance on activation quantization. NoisyQuant achieves the first success in actively refining the distribution being quantized to reduce quantization error following the theoretical results on additive noisy bias, with minimal computation overhead.
- Demonstrates consistent performance improvement by applying NoisyQuant on top of existing PTQ quantizers.
3. Method
3.1. Preliminary - PTQ in ViT
- Dominance of FC linear projection layers in transformer models: $f(X) = WX + B$
- Main computation burden $WX$ → Replace floating-point MACs with much cheaper fixed-point ops.: $f_q(X)=q_W(W)q_A(X)+B$
- Main problem: The heavy-tailed activation distribution of $X$ causes significant quantization error between $X$ and $q_A(X)$ at low precision
- Previous PTQ methods: Modify the design of quantizer $q_A(\cdot)$
- Ours: Modify the dist. of activation $X$ with a pre-sampled noisy bias before quantization.
3.2. Theoretical analysis on quantization error
⚔️ A straightforward way to alter the input activation dist. is to add a fixed “Noisy Bias” sampled from a Uniform random dist.
⚔️ Theorem 1. → Basically showing that Noisy Bias’ quantization error is always smaller than that of doing nothing, when $x$ is in a certain range (close to the center of the quantization bins) 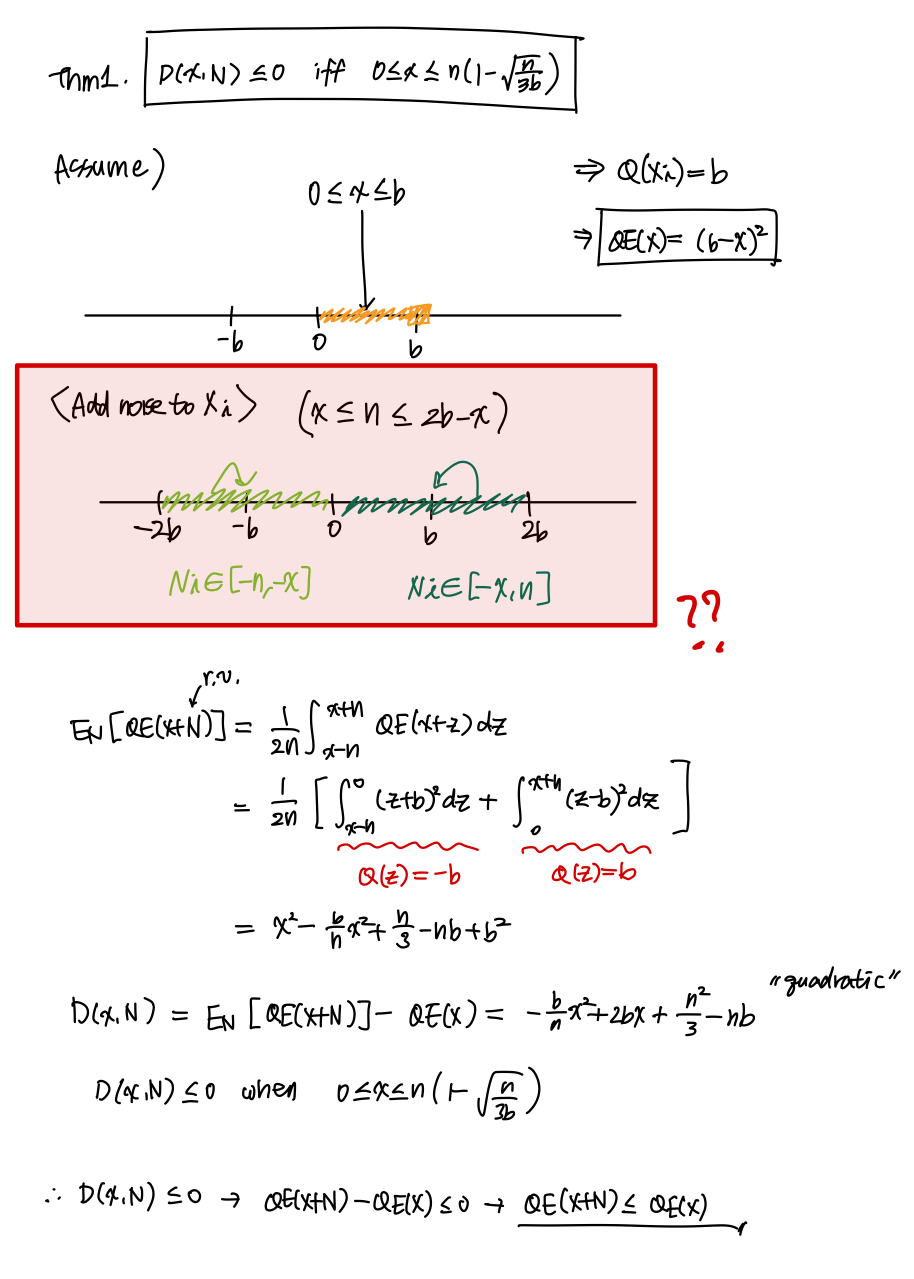
⚔️ Theorem 1 indicates that adding Noisy Bias can always reduce the quantization error of elements close to the center of the quantization bin, which is the source of large quantization error in a heavy-tailed distribution.
3.3. NoisyQuant formulation and pipeline
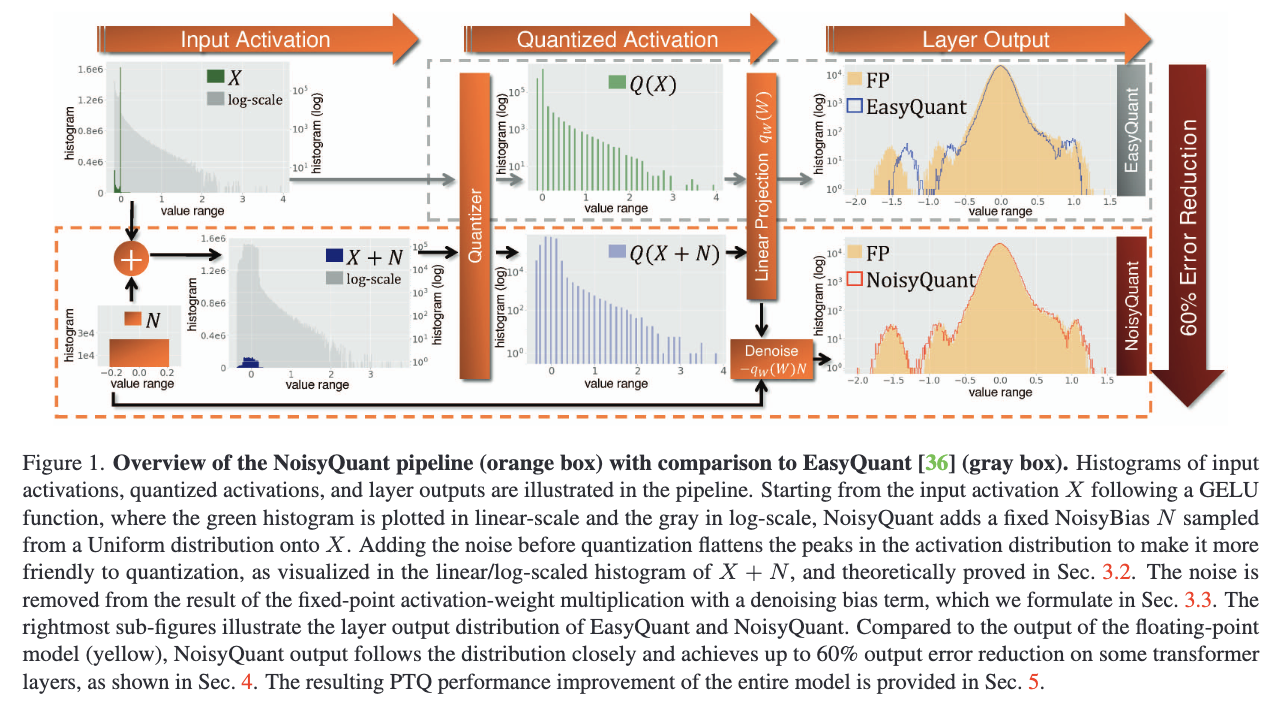
⚔ Steps of NoisyQuant
- Before PTQ, sample a single Noisy Bias $N \in \mathbb{R}^{m\times 1}$ from a Unifrom dist. for each layer , and fix it throughout the inference.
- Range of $N$ is determined by the calibrationi objective defined in some equation in Sec. 3.2.
- At inference time (PTQ), add Noisy Bias $N$ to the input activation $X$, altering the dist. being quantized to reduce the input quantization error.
- After matmul, remove the impact of $N$ by adjusting the bias term with a denoising bias, retrieving the correct output.
- NoisyQuant FC computation: $f_{N_q}(X)=q_W(W)q_A(X+N)+(B-q_W(W)N)$
- $N$ is fixed throughout inference, therefore $B’=B-q_W(W)N$ only needs to be computed once before deployment → No computation overhead in the inference process
- Only computation overhead brought by NoisyQuant: on-the-fly summation of $X+N$
⚔ $B’$ and $N$ stored in INT16 to enable integer-only inference.
⚔ Noisy Bias enablex $X+N$ to have a lower quantization error than $X$ → We can also achieve lower output quantization error.
4. Theoretical insight verification
4.1. Empirical verification of Theorem 1
5. Experiments
5.1. Experimental settings
⚔️ Dataset
- ImageNet for classification tasks, MSCOCO for object detection tasks.
- For both tasks, 1024 images are randomly sampled as calibration data for all PTQ methods
⚔️ Pretrained model architecture
- Uniform 6-bit and 8-bit PTQ on pretrained ViTs.
- Classification: ViT, DeiT, and Swin by the Timm library
- Detection: DETR w/ ResNet-50 backbone
⚔️ Implementation Details
- Quantizes all weights/inputs involved in matrix multiplication (qkv-projectors, attention output projectors, MLPs, linear embeddings, and model heads) + input activation of linear layers and matmul operators
- Keep layer normalization/softmax operation full precision
- Symmetric layer-wise quantization for activations and symmetric channel-wise quantization for weights; weights are quantized by MinMax values w/o clamping
- We implement NoisyQuant on top of linear quantizer EasyQuant and nonlinear quantizer PTQ4ViT
- We decide the params. of the Noisy Bias distr. through linear search
5.2. NoisyQuant performance
- It is worth noting that although nonlinear quantizer like PTQ4ViT consistently achieves higher PTQ performance than the linear EasyQuant quantizer, the enhancement brought by NoisyQuant enables the NoisyQuant-Linear quantizer to achieve on-par or even better performance than the nonlinear PTQ4ViT, with much lower overhead in hardware deployment.