EagleEye: Fast Sub-net Evaluation for Efficient Neural Network Pruning

2024-07-13

Keywords: #noise #activationdistribution

1. Introduction

Pruning: Aims to reduce computational redundancy from a full model with an allowed accuracy range.
Searching
- Goal: Obtain the sub-net with highest accuracy with small searching efforts
- Evaluation process: Aims to unveil the potential of sub-nets so that best pruning candidate can be selected to deliver the final pruning.
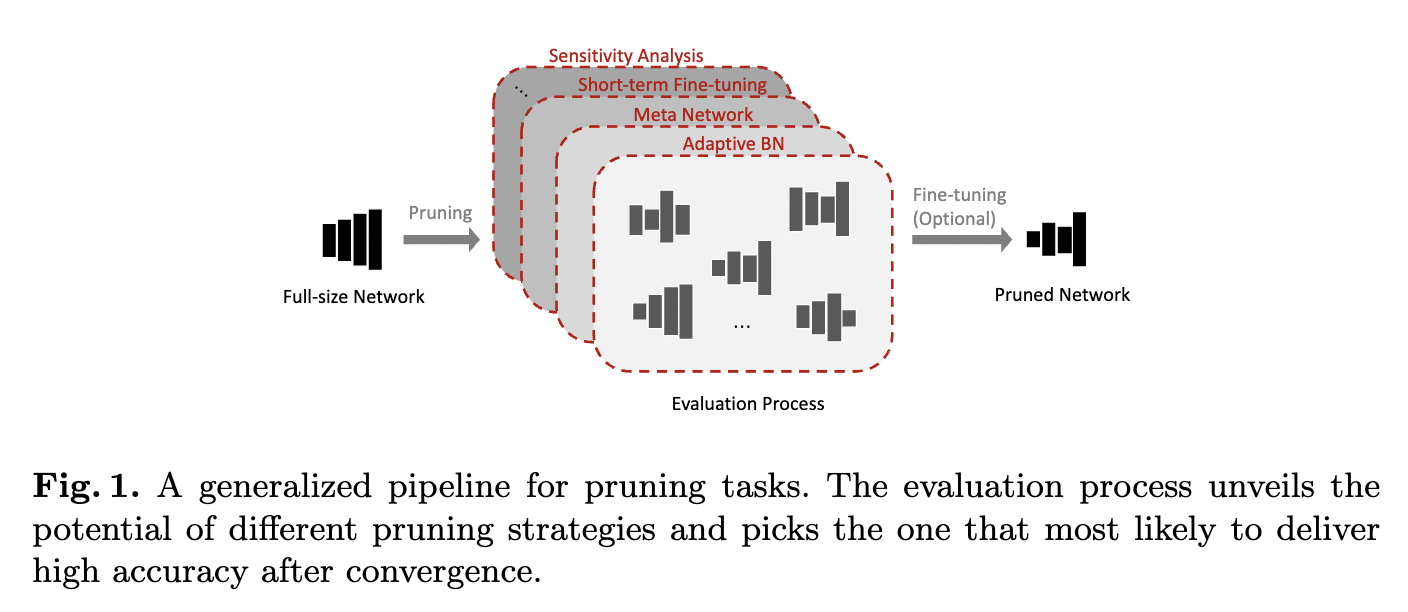
Problem: Evaluation methods in existing works are sub-optimal (inaccurate or complicated)
- Inaccurate: The winner sub-nets do not necessarily deliver high accuracy when they converge.
  - Why? Correlation problem measured by several commonly used correlation coefficients / Sub-optimal statistical value for BN layers.
  - How to solve? Adaptive BN to effectively reach a higher correlation for the proposed evaluation process.
- Complicated: The evaluation process in some works rely on computationally intensive components, or hard to tune the hyperparameters.
  - e.g. reinforcement learning agent, auxiliary network training, knowledge distillation, etc.
Contributions
1. Identify the reason behind so-called vanilla evaluation step in many existing pruning methods leads to poor pruning results. First to introduce a correlation analysis to the domain of pruning algorithm.
2. Propose the technique of adaptive batch normalization. It is one of the modules in our proposed pruning algorithm called EagleEye.
  - Effectively estimate the converged accuracy for any pruned model in the time of only a few iterations of inference.
  - General enough to plug-in and improve some existing methods for performance improvement.
  1. Experiments show that although EagleEye is simple, it achieves the state-of-the-art pruning performace.

3. Methodology

3.0 Typical pipeline for NN pruning

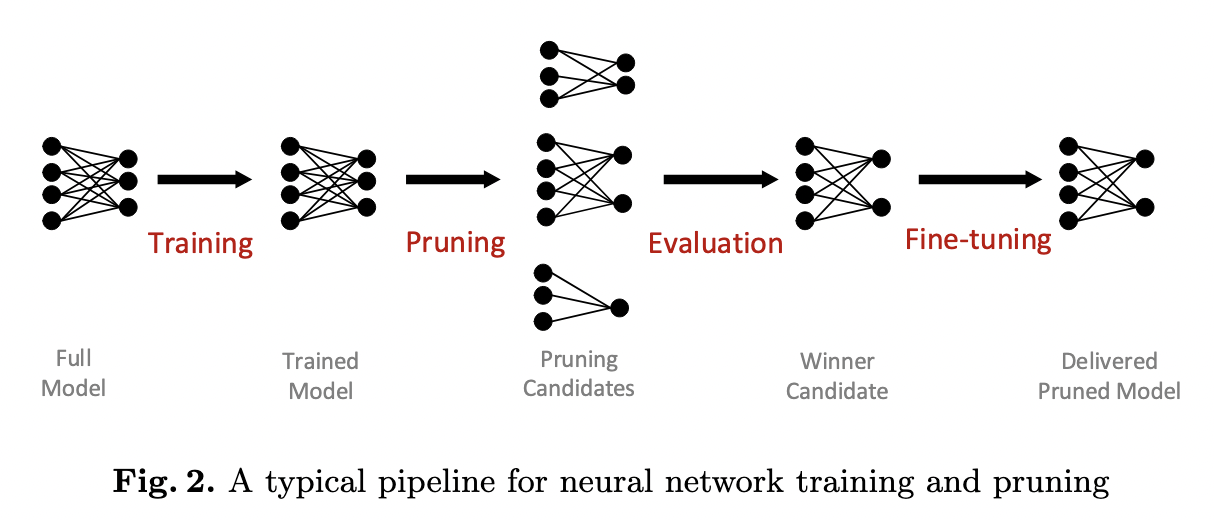
⚔️ Objective of Pruning

$\left(r_1, r_2, \ldots, r_L\right)^*=\underset{r_1, r_2, \ldots, r_L}{\arg \min } \mathcal{L}\left(\mathcal{A}\left(r_1, r_2, \ldots, r_L ; w\right)\right), \quad \text { s.t. } \mathcal{C}<\text { constraints }$

$\mathbb{L}$ is the loss function, $\mathbb{A}$ is the NN model.
$r_l$ is the pruning ratio applied to the $l^{th}$ layer.
Given some constraints $\mathbb{C}$ (e.g. targeted amount of parameters, operations, or execution latency), a combination of pruning ratios $(r_1, r_2, …, r_L)$ is referred as pruning strategy.
All possible combinations of the pruning ratios form a searching space.
We consider the pruning task as finding the optimal pruning strategy, denoted as $(r_1, r_2, …, r_L)^{*}$, that results in the highest converged accuracy of the pruned model.

⚔️ Existing Searching Methods: Greedy algorithm, RL, Evolutionary algorithm

3.1 Motivation

Subnets with high evaluation accuracy are selected, with the expectation that this high performance translates to after fine-tuning. → However, there exists a significant gap before and after fine-tuning, making evaluation accuracy unreliable when choosing winner candidate. (?? Hard to understand some parts of the motivation.)
Turns out, BN layers largely affect the evaluation accuracy.
→ Why? Vanilla evaluation uses BN inherited from the full-size model.
→ The outdated statistical values of BN layers:
1) drag down the evaluation accuracy to a surprisingly low range.
2) break the correlation between evaluation and final converged (after fine-tuning) accuracy

⚔️ Basics of BN layers

3.2 Adaptive Batch Normalization

Applying global BN statistics (stats w.r.t. full model) to pruned networks lead to low-range accuracy.
Re-calculate $\mu_T$ and $\sigma_T^2$ with adaptive values by conducting a few iterations w.r.t. the training set, which adapts the BN stats to the pruned network connections.
- Freeze all network params. while resetting the moving average stats.
- Update the moving stats by a few iters. of foward-prop, but without backward-prop
- Adaptive BN stats: $\hat{\mu_T}$ and $\hat{\sigma_T^2}$

⚔️ Correlation between accuracy of [vanilla eval - fine-tuning] (left), [adaptiveBN - fine-tuning] (right)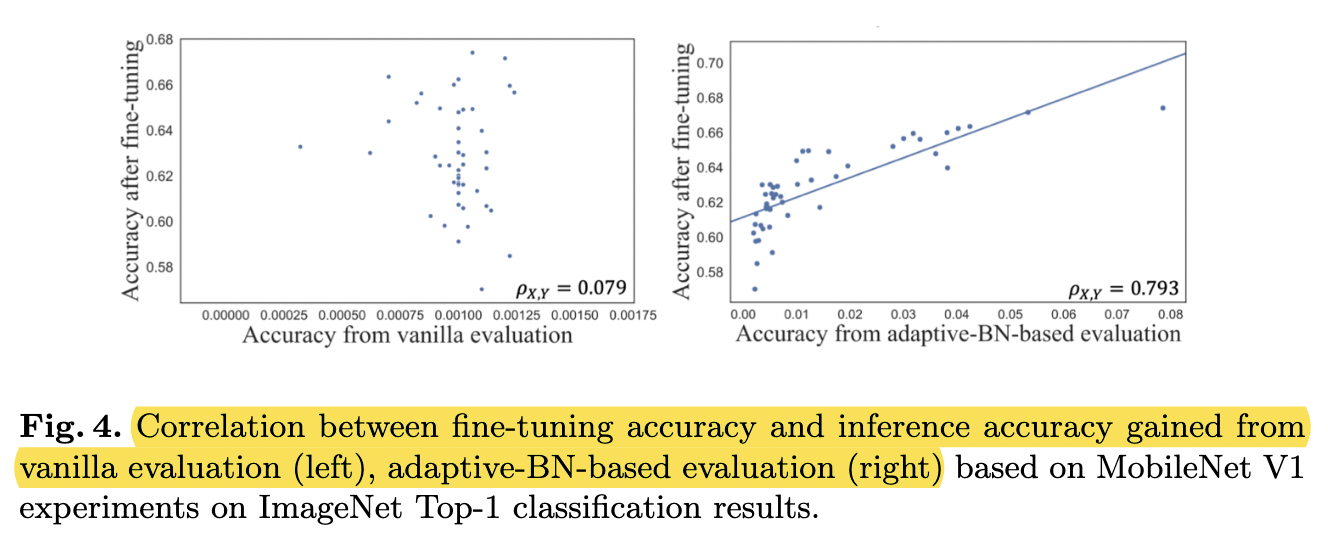

⚔️ Distance between [global BN stats - val BN stats] (a,c) which has big difference, [adaptiveBN stats - val BN stats] (b,d) which has little difference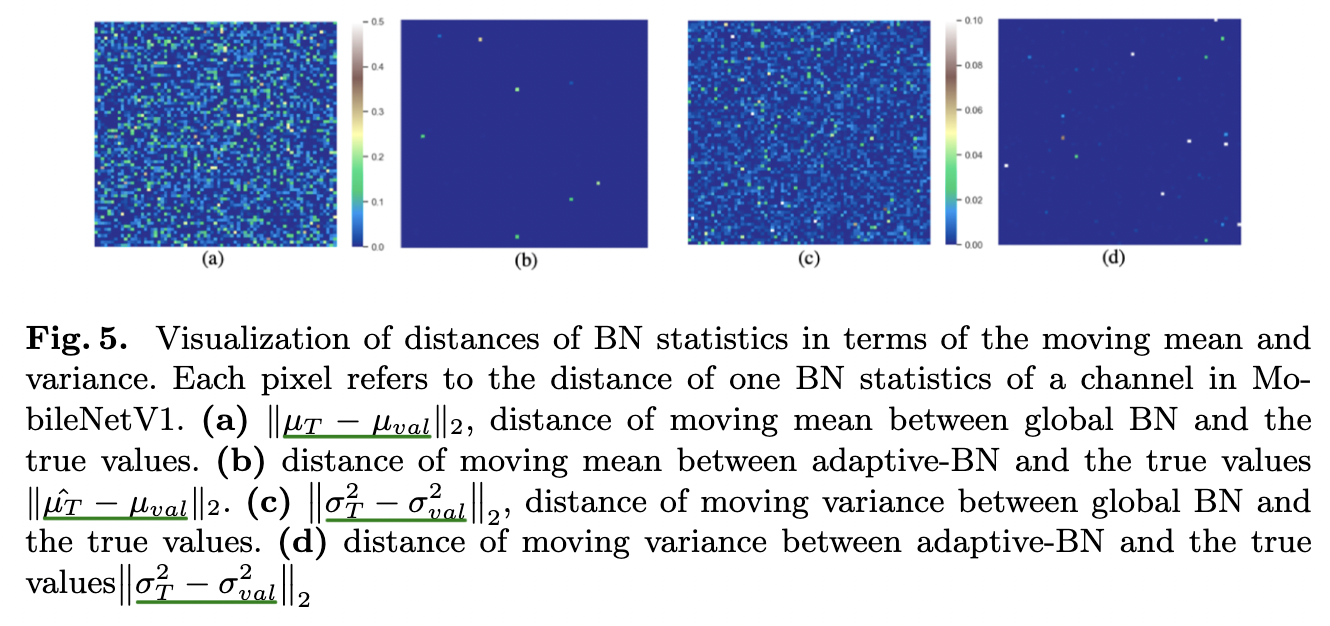

3.3 Correlation Measurement

Pearson Correlation Coefficient
Spearman Correlation Coefficient, and Kendall rank Correlation Coefficient

3.4 EagleEye pruning algorithm

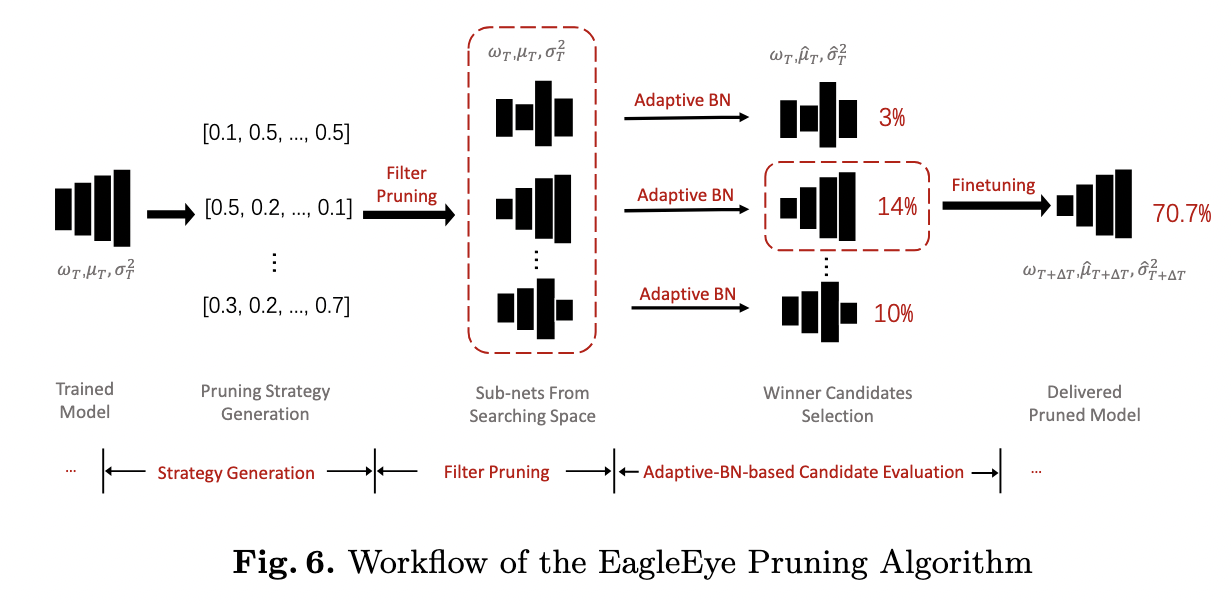
Strategy generation
- Outputs pruning strategies in the form of layer-wise pruning rate vectors like $(r_1, r_2, …, r_L)$ for a $L$-layer model.
- Constraints: Inference latency, FLOPs, # of parameters
- Random sampling is good enough to quickly yield pruning candidates w/ sota accuracy. → adaptiveBN takes the burden, so the efforts of generating candidates are allowed to be massively simplified (a guess)
- Low computation cost, fast speed
Filter pruning process
- Prunes the full-size trained model according to the generated pruning strategy.
- Filters are ranked according to their L1-norm, and the $r_l$ (pruning rate of $l$th layer) of the least important filters are pruned.
The adaptive-BN-based candidate evaluation module
- Given a pruned network, it freezes all learnable parameters and passes a small amount of data in the training set to calculate the adaptive BN stats $\hat{\mu}$ and $\hat{\sigma^2}$.
- In practice, 1/30 of the training set is used.
- Next, model evaluates the performance of the candidate networks on a small part of the training set- called sub-validation set, and picks the winner.

4. Experiments

4.4 Effectiveness of our proposed method

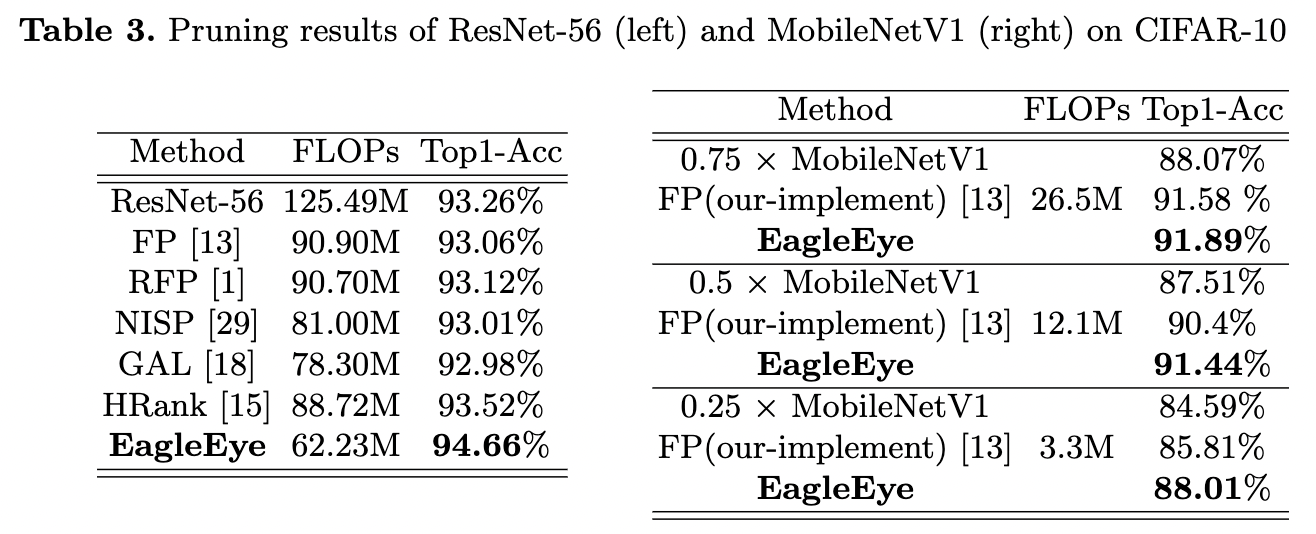
⚔️ Top-1 accuracy on CIFAR-10.

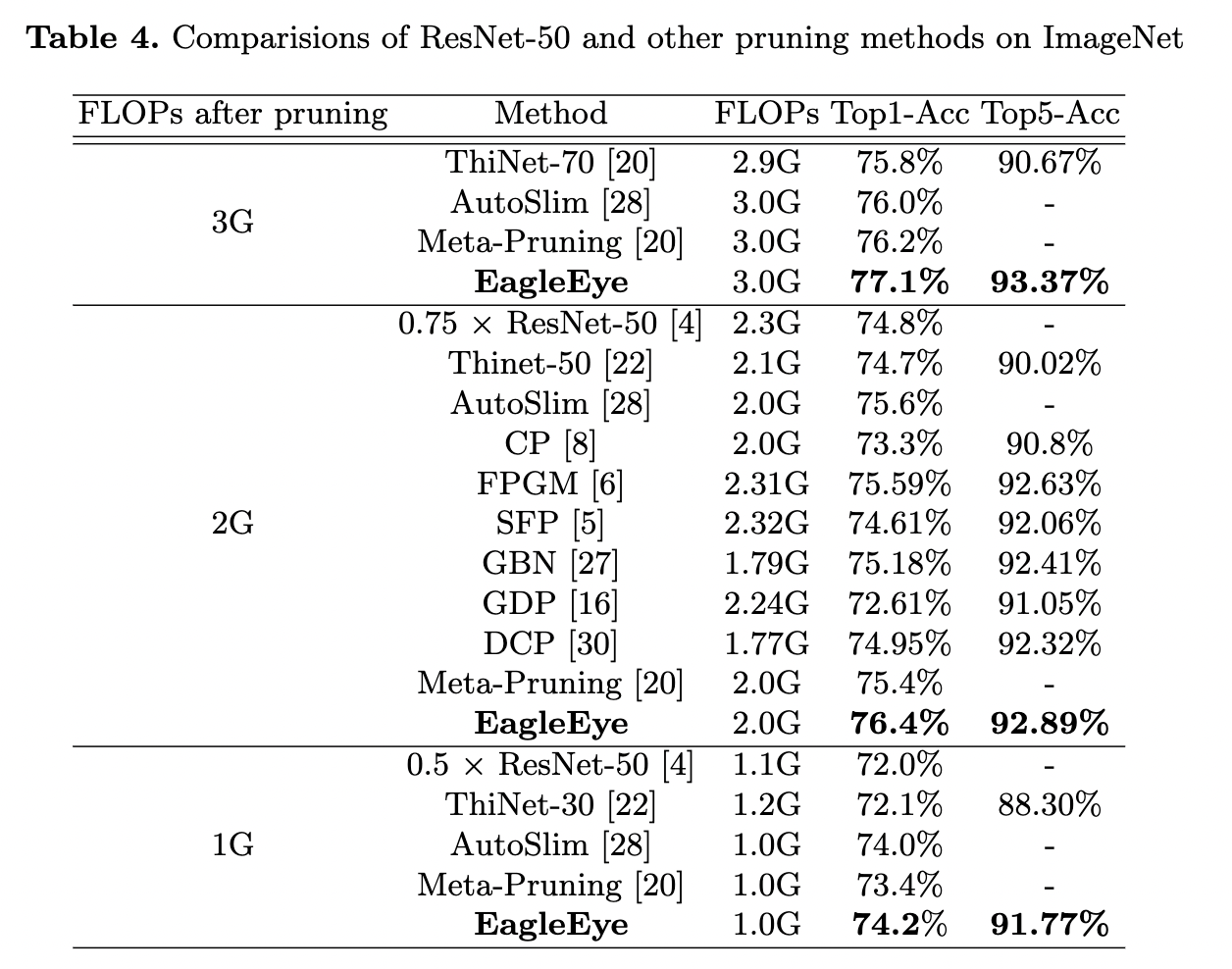
⚔️ Accuracy w/ FLOPs constraint on ImageNet (Big dataset).

For each FLOPs constraint (3G, 2G, and 1G), 1000 pruning strategies are generated.
Finetune the top-2 candidates and return the best as delivered pruned model.

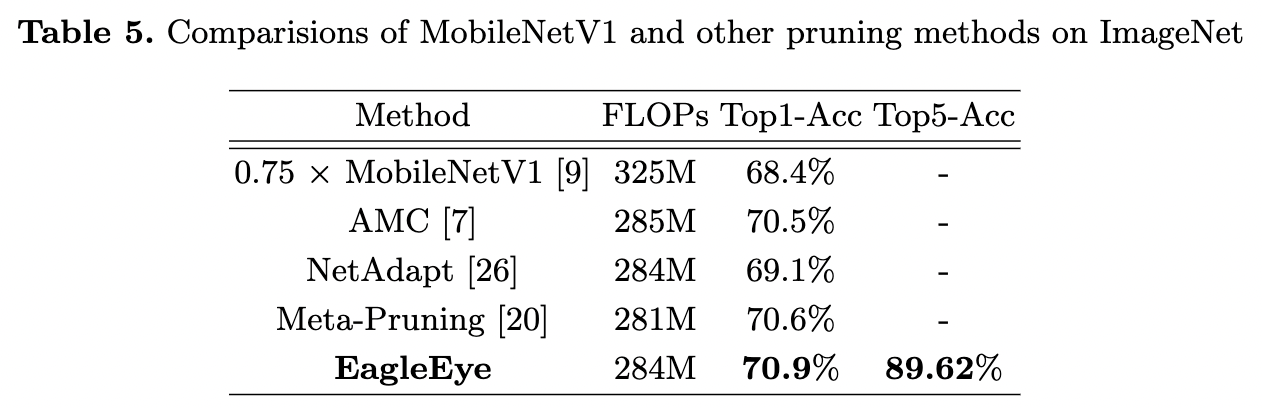
⚔️ Accuracy on MobileNetV1 (compact network) on ImageNet.

Under the same FLOPs constraint (about 280M FLOPs)
Goes throught the same process like the above ImageNet experiments.