Kalman Filter

🍇 Why do we need a Kalman Filter?

To estimate the position of a robot precisely.
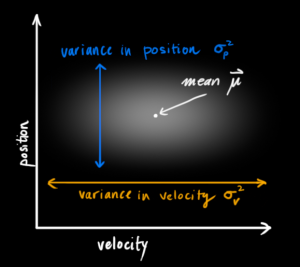
The state of a robot is portrayed as (position, velocity)
Position and velocity both have some sort of uncertainty, which can be interpreted to some form of a Gaussian distribution.

🍇 Correlation between position and velocity

In real life, position and velocity has some sort of correlation.
ex) lower velocity leads to shorter distances, and higher velocity leads to further distances
The goal for Kalman filter
→ Finding the correlation between position and velocity
→ This correlation is called a ‘covariance matrix’


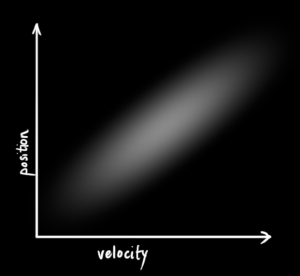Uncorrelated	Correlated

🍇 How Kalman Filter Works - the math

🏳️ Finding the prediction matrix , \(F_k\)

Let \(\hat x\) be the state function.
\[\hat x_k = \begin{bmatrix} p_k\\ v_k \end{bmatrix}\]
Transformation Matrix : the matrix that uses the past state \((p_{k-1}, v_{k-1})\) to estimate the current state \((p_{k}, v_{k})\)
\[\hat x_k = F_k \hat x_{k-1}\]
If all is true, the following can be said.

\[\begin{matrix} p_k = p_{k-1}+\Delta t v_{k-1}\\ v_k = v_{k-1} \end{matrix}\] \[F_k = \begin{bmatrix} 1 & \Delta t\\ 0 & 1 \end{bmatrix}\]

🏳️ Covariance Scaling

🏳️ Finding \(p-v\) Covariance

Covariance between position and velocitiy is like the below:
\[P_k = \begin{bmatrix} pp & pv\\ vp & vv \end{bmatrix}\]
Now, with the prediction matrix and covariance scaling we can derive the formula.
\[\hat x_k = F_k \hat x_{k-1}\] \[Cov(Ax)=ACov(x)A^T\] \[P_k = F_k P_{k-1}F_k^T\]
proof

🍇 External Factors