R2 Loss: Range Restriction Loss for Model Compression and Quantization

2024-08-17

Keywords: #Activation #Batch Normalization

1. Introduction

Premise: Quantization bit-resolution is inversely proportional to the range of weights and effects accuracy.
Problem: Since outliers tend to increase range, outliers are detrimental for quantization friendly models.
Intuitive overview of the problem & solution:
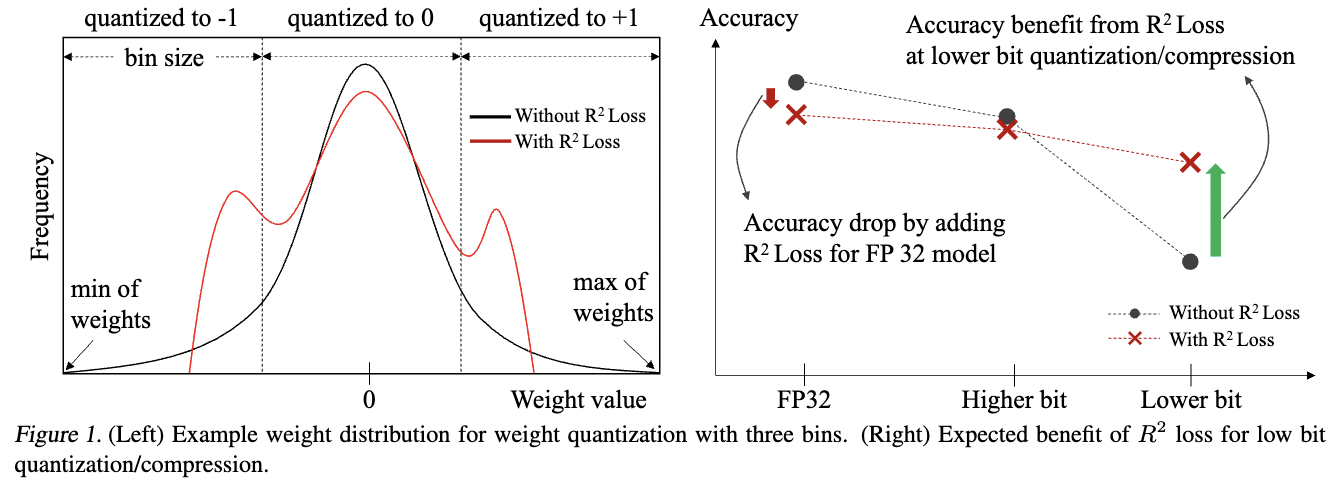
Solution: Range Restriction Loss ($R^2$ loss)
- Regress FP32 model’s accuracy slightly as it works as additional weight regularization like weight decay.
- Quantization-friendly weight distribution removing outlier weights, so lower bit quantization accuracy can be improved.
Justification for R2 loss having limited benefits for higher bit quantization: SOTA also shows reasonable accuracy regression, leaving little room for improvement.
Contributions
- R2 Loss: Simple and intuitive way to penalize outlier weights during pre-training.
- Margin R2 Loss: Penalizes weights larger than a margin, while minimizing the width of the margin.
- Soft-Min-Max R2 Loss: Smoothly penalize not only outliers but also near- outlier weights.
- R2 Loss, Margin R2 Loss → More effective to symmetric quantization.
- Soft-Min-Max R2 → More effective for others (e.g. model compression) as it makes asymmetric weight distribution.

3. Range Restriction Loss

Goal: R2 Loss is an auxiliary loss to reduce the range of weights for every layer to get better pre-trained models for further quantization.
Invariant to the quantization technique.
Reference: KURE RobustQuant
$R^2$ loss is employed during training of the base model itself and not during quantization.
The purpose of $R^2$ loss is to provide effective initial weights for quantization.

3.1 $L_{\infty} R^2$ loss

$L_{r e g}=\sum L_{\infty}(W)$

Penalize only the outliers by adding $L_{\infty}(W)$ as an auxiliary loss for every layer in the model.
Brings the overall range of weight down in contrast to KURE.
Also makes the weight distribution similar to a mixture of Gaussians as seen in KURE.

3.2 Margin $R^2$ Loss

$L_{r e g}=\sum(|M|+\max (|W|-|M|, 0))$

Define a margin for the range of allowed weights.
The width of the margin + Weights outside the margin is simultaneously penalize. -> Ensure that the range of the overall weight distribution is small.
$M$ is a learnable parameter per layer.
Difference from $R^2$ Loss: Margin $R^2$ Loss penalizes all weights outside the margin versus $R^2$ Loss penalizes only the maximum weight.

3.3 Soft-min-max $R^2$ Loss

$\begin{aligned} s_{\max } & =\frac{\Sigma\left(W \odot e^{\alpha \times\left(W-W_{\max }\right)}\right)}{\Sigma e^{\alpha \times\left(W-W_{\max }\right)}} \\ s_{\min } & =\frac{\Sigma\left(W \odot e^{-\alpha \times\left(W-W_{\min }\right)}\right)}{\Sigma e^{-\alpha \times\left(W-W_{\min }\right)}} \\ L_{\text {reg }} & =\left(s_{\max }-s_{\min }\right)+e^{-\alpha} \end{aligned}$

Eliminate the constraint on the magnitude of weights and strictly enforce it on the range of weights. → Improve asymmetrically quantized models.
Temperature $\alpha$ is a learnable parameter per layer.
- $e^{-\alpha}$ term in the loss goes to 0 as training progresses, making $L_{reg}$ to approach hard min-max loss.
- Smooth penalization possible.
Penalizes near-outlier weights together rather than strictly brining only outliers down like other $R^2$ losses. → More susceptible to outliers.

4. Experiment

4.1. Experiment settings

Pre-training from scratch w/ and w/o $R^2$ Loss
- Train ResNet-18, MobileNetV1/V2 on ImageNet with R2 Loss to get pretrained models before model compression and QAT. → Compare with pre-trained models of ResNet-18 from Torchvision.
- Use modified versions of ResNet-50, -101, MobileNetV1/V2 for better FP32 performance. → Tain from scracth w/ and w/o $R^2$ Loss.
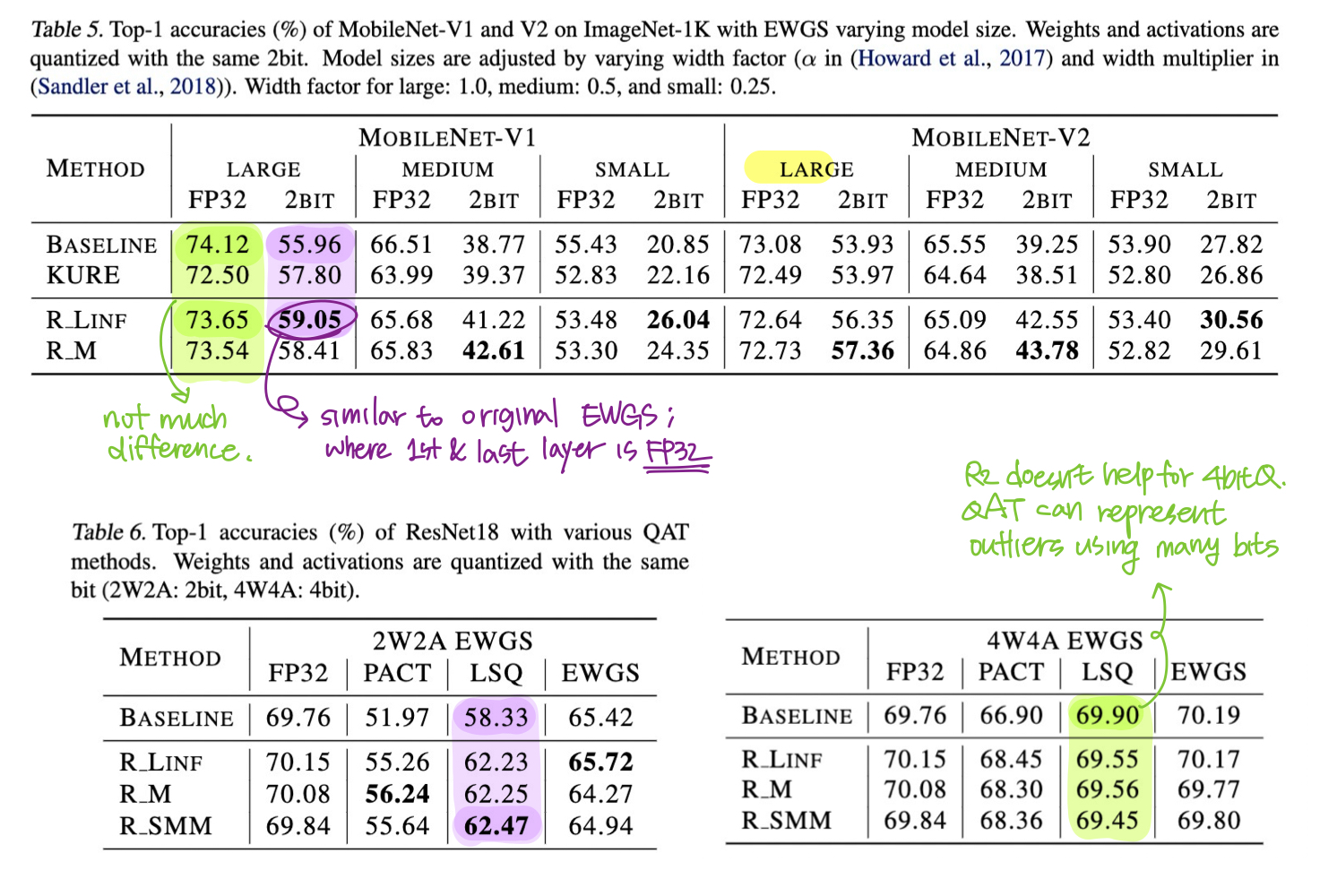
- Table 5 shows that $R^2$ loss does not significantly affect FP32 model performance.
Model Compression and Quantization
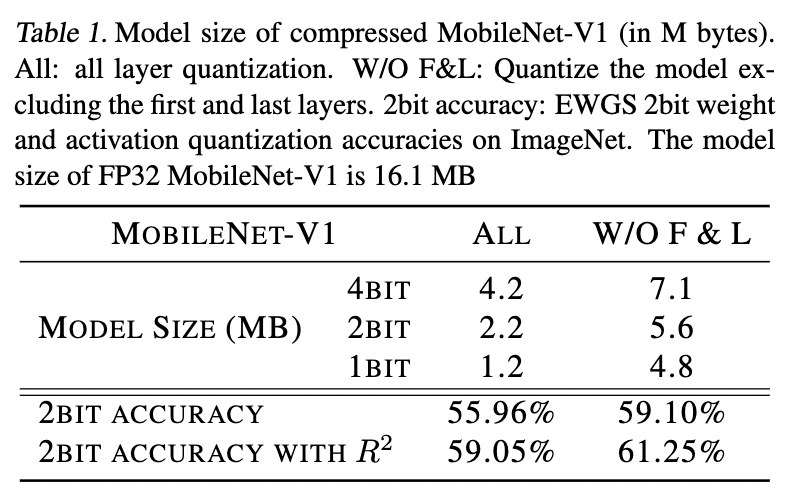
- Apply compression and quantization for all layers including the first and last layers. (★)
- Storage benefits and performance when including and not including first and last layer quantization is shown in Table 1.

4.2. Model Quantization

PTQ with $R^2$

QAT with $R^2$

PACT: Train from scratch using $R^2$ loss.

EWGS, LSQ: Initialize model to pre-trained ResNet-18, MobileNetV1/V2 with $R^2$ loss.

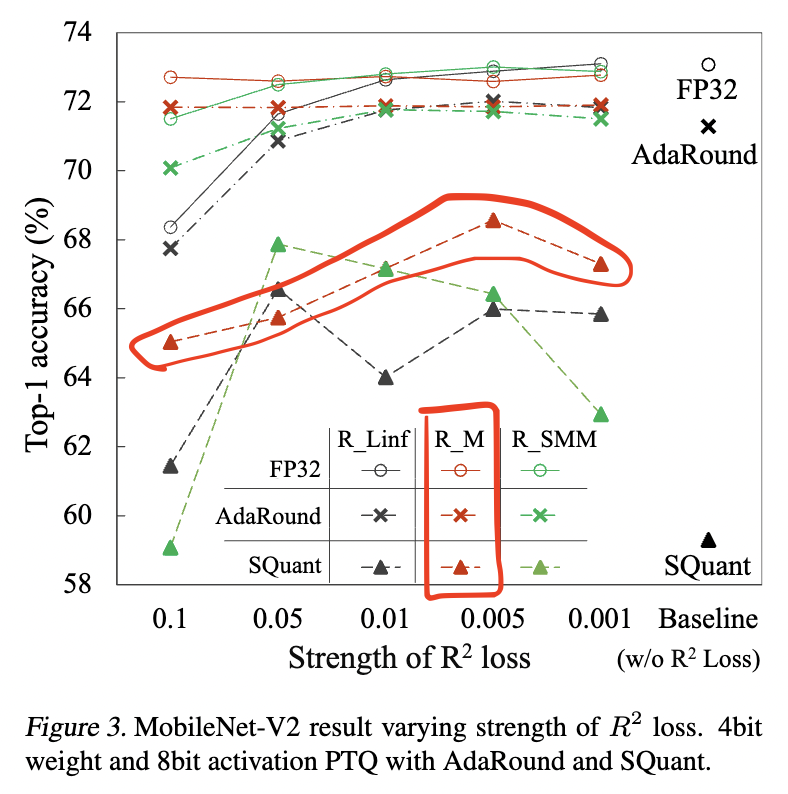
4.4. Strength of $R^2$ loss & comparison between $R^2$ loss

Strength of $R^2$: Accuracy from a model trained with Margin $R^2$ loss is more consistent and better than $L_\infty$
Recommend to use Margin $R^2$ loss for symmetric quantization if it is hard to find proper strength for $L_\infty R^2$ loss.

5. Conclusion

R2 Loss is a technique to get rid of outliers. → This serves as a good initialization for SOTA PTQ, QAT, and compression techniques.
While FP32 accuracy can slightly regress as R2 Loss penalizes outliers, it significantly improves quantization accuracy for ultra low bits.