PTMQ: Post-training Multi-Bit Quantization of Neural Networks
2024-08-11
Keywords: #Activation #Batch Normalization
1. Introduction
- QAT multi-bit quantization problems (★★★)
- Time-consuming
- When switching bit-width, BN stats. need to be recalulated (AdaptiveBN) → affects the real-time response of multi-bit quantization.
- PTQ approaches: Minimizing discrepancy between FP32 and quantized feature maps using MSE, cosine distance.
- Searching for quantization scale factors.
- Insufficient for achieving robust multi-bit quantization
- Full-parameters fine-tuning can lead to overfitting with limited data.
- Optimizing rounding values. → Promising, but challenging.
- Searching for quantization scale factors.
-
Folding norm layers with previous layers helps mitigate the influence of statistical parameters.
-
PTMQ pipeline
- Contributions
- Propose PTMQ, a PTQ multi-bit quantization framework. PTMQ supports uniform and mixed-precision quantization, and can perform real-time bit-width conversion.
- Propose Multi-bit Feature Mixer (MFM), which enhances the robustness of rounding values at various bit-widths by fusing features of different bit-widths.
- Introduce Group-wise Distillation Loss (GD-Loss), to enhance the correlation between different bit-width groups, improving overall quantization performance of PTMQ.
- Experiments conducted on CNN and ViT backbones.
2. Related Works
- Rounding-based PTQ: optimizing 1) rounding value, 2) scaling factor
- AdaRound (2020): Learning the rounding mechanism by analyzing the second-order error term. → Proposes layer-by-layer reconstruction of the output.
- BRECQ (2021): Extends AdaRound to block-wise reconstruction.
- Qdrop (2022): Higher accuracy can be achieved by randomly dropping quantized act. values and incorporating act. quant. into the weight tuning.
- FlexRound (2023): Weights can be mapped to a wider range of quantized values, rather than being limited to only the nearby 0 or 1 values.
- Problem: They can only quantize one specific bit-width at a time, not directly accessible to perform multi-bit quantization.
- Multi-Bit Quantization:
- RobustQuant (2020): Uniformly distributed weight tensor is more tolerant to quantization, higher SNR, and less sensitive to specific quantization settings than normally-distributed weights → Proposes kurtosis regularization RobustQuant
- Any-Precision: Trains using DoReFa, and the quantized model is stored in FP32. In runtime, this model can be set to different bit-width by truncation. Any-Precision DNN
- MultiQuant (2022): Addresses vicious competition between high-bit-width and low-bit-width quantization → Proposes adaptive soft-labeling strategy
- Problem: Previous methods focus on QAT.
3. Approach
3.1 PTMQ Modeling
-
Multi-bit quantization model formulation:

-
For PTQ, quantization parameters are usually optimized as block-independent sequences.

-
PTQ aims to learn robust rounding values and stand-alone quantization step size.
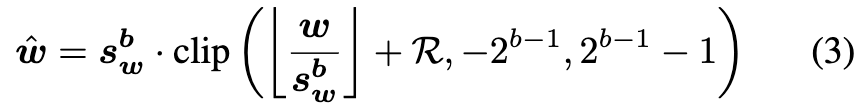
-
$\mathbb{R} \in {0,1}$: The rounding value for up or down in inference.
3.2 The Pipeline of PTMQ
- Scaling factors are initialized. Block-wise optimization is adopted for reconstruction.
- Bit-width configuration $\mathbb{B}$ is divided into three groups; Each require different scaling levels of tuning during reconstruction.
- During reconstruction of a block, a random bit is selected for each bit group. (Inputs) = (The integration of output features from different bit groups) -> through Multi-bit Feature Mixer
- (Output of block undergoing reconstruction) = (Sample random bits from each bit group)
- Reconstruction loss = Sum of all loss of sampled bit-widths.
- Rounding values/act. step size within block optimized by back-prop. - PTMQ aims to enhance robustness of quantized block by improving lower & upper performance bound.
3.3 Opimization-based Multi-Bit Quantization
Absorb Multi-Bit Errors into Rounding Values
- Activation quantization: $\hat a = a (1+u)$ -> $u$ affected by bit-width and rounding error.
- Transfer noise; activations to weights: $w[a\odot (1+u(x))] = [w\odot(1+v(x))]a$
- Similarly, quantization noise $(1+\tilde{u}(x))$ (due to activation & multi bit-widths) can be transposed to weight perturbation $(1+\tilde{v}(x))$ = \mathbb{R}
- Intuition: Activation quantization & multi bit-width = Introducing multi-bit quantization errors into the network weights = Absorbed by rounding values.
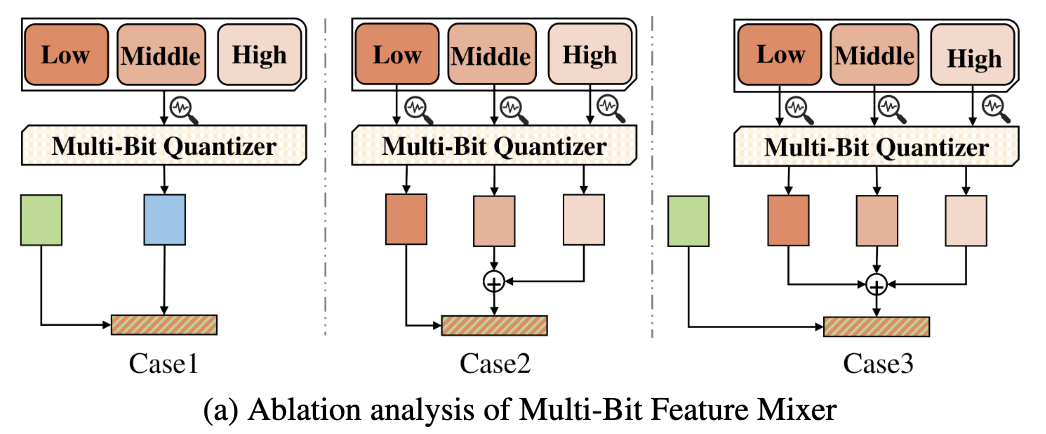
Multi-Bit Feature Mixer
- Mixing features of multi-bit quantization as inputs enhance the robustness of rounding values for various bit-widths.
- Case 1) Randomly select one type of feature among L/M/H bit-width groups, and fuse it with FP features through random dropout (Qdrop, 2022).
- Case 2) Random bit features sampled from each group. -> H features mixed M features through addition -> Randomly replace with L features and produce fused feature.
-
Case 3) Random bit features sampled from each group and mixed with addition. -> Fused with FP features by random dropout. (★ Most effective! ★)
- Key point: Input of the reconstruction block combines multiple quantization features instead of only biasing towards one quantization feature.
- Formulation of MFM: